The Language of Computers Part 1

Language Services Direct Team

Does this statement make sense to you?

‘There are only 10 types of people in the world: those that understand binary, and those that don’t.’

It might be that you have no idea how ‘10’ becomes two different options, or maybe you will instantly see the connection to binary code. But do you fully understand the implied joke hidden in this statement?

One person who would have known exactly what was going on was coding extraordinaire Alan Turing, the ‘father of computer science and artificial intelligence’. He is the face of the new £50 note, and the inspired design includes its own hidden message: Turing’s birthday, unfurling on a binary-coded banner. While it may look like a random stream of zeroes and ones, if you understand how binary code works you can crack the code and reveal this significant number.

If you still feel mystified, fear not: this article provides a quick crash course in making sense of the language of our computers, helping you to make sense of the joke above (and read the binary number on the new £50 note!).

What Is Binary Code?

The binary number system has existed since before the computer – in fact, it is ancient history! Over time, the binary number system has been refined by notable mathematicians, but it was the advent of the computer that saw it become a fundamental basis for communicating and storing information.

Binary code is the basis for pretty much all modern computer programming. But why are we even concerned with binary code, you might wonder? Well, it is not exactly the same type of language we usually talk about – those more familiar languages such as French, German, Spanish, and Mandarin, for example. But binary code is a language of sorts – in fact, it is the language that makes it possible for you to be reading this article on your computer, tablet or smartphone. Therefore, it is a fundamental language for any futureproof business to be aware of, even if computer programmers are not on your current payroll.

Making Sense of Binary Code

Binary code is a number system based on just two elements, the 0 and the 1. You can think of it like an on-off switch, where 0 is ‘off’ and 1 is ‘on’. In practical terms, it is the ‘1’ values that you count to find the meaning within the code.

The binary number system is a base 2 number system. To put this into context, the normal way of viewing numbers in our day-to-day lives uses a decimal (or base 10) number system – there are 10 digits, numbered 0 to 9. These 10 digits make up the decimal number system, while 0 and 1 make up the binary number system.

When you count in decimals, the addition of a new ‘level’ (such as going from single to double digits, and then to triple digits) means your number is 10 times bigger: 10 is 10 times bigger than 1, 100 is 10 times bigger than 10, and so on. However, with binary code, the addition of an extra level (or ‘bit’, to bring in some computing terminology) means that the number becomes twice as big.

This chart shows how numbers in a decimal system grow by 10 times as you add an extra digit. The row below shows the value of the first four binary code digits (growing by 2 times with each digit). Interestingly, the following row shows that the binary code outputs for 8, 4, 2 and 1 match the decimal numbers 1000, 100, 10 and 1 in appearance!

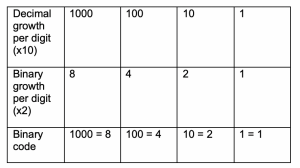
Leaving thoughts of the decimal number system behind, how is it that the four binary code digits ‘1000’ can equal 8? The trick here is to remember the zeroes. You also need to remember to read a binary number from right to left. For example, the following chart shows the base 2 levels (which double with every digit) as a familiar numerical value (starting with 1, doubling to 2, then to 4, then to 8 and finally to 16). Underneath, the corresponding binary code for ‘8’ appears.

The reason that we can know this is 8 is because it is the only countable value (represented by a 1) – so it is ‘on’ rather than off. You need to have the following three zeroes after the 1 though (so 1000 rather than just 1) – these show that the countable number is in the ‘8’ position. To make head or tail of a binary number, you have to think about the position of each 0 and 1, and its corresponding value.

Going back to the joke at the start of the article, you may now be able to see that ‘10’ equals 2 in binary code – the 0 is in the 1 position, so it is not counted, and the 1 is in the 2 position, so it is counted, which therefore equals 2!

‘10’ = 2 + 0 = 2

POP QUIZ

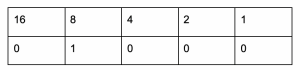
Fancy testing your new-found knowledge? Try using this approach to figure out the number depicted by each of the following binary codes:

1. 10101
2. 01001

Both of these examples have five digits, so the previous chart might help you total the values. Answers at the end of this article!

Binary Code in Action

You can do so much with zeroes and ones if you have the know-how. For example, computer programmers use more complicated programming languages (which make binary code more manageable and readable) to create things like computer programs, apps and web plug-ins. In other words, this code is just as valuable to your business as any foreign language, even if it underpins your business offering in very different ways.

Binary code may seem like a much more of a foreign language than French or German, but it is the behind-the-scenes language that holds our global communications together in this digital age. In our next article, we will revisit the topic of computer coding, looking at some of its applications in more detail.

What Language is Important for Your Team?

While binary and programming aren’t in our suite of languages, we can help you with ensuring everyone on your team can communicate with each other in the real world.

Get in touch to discuss what languages are important in your teams.

 

Pop Quiz Answers:

1. 21 (16 + 4 + 1)
2. 9 (8 + 1).